Blog

Medidas Mecânicas e Incertezas

Índice

O LabCalc representa um conjunto de ferramentas desenvolvidas ao longo da minha carreira como professor e coordenador do Laboratório de Física na UVV (Universidade Vila Velha do ES), com o propósito de harmonizar as metodologias matemáticas utilizadas e viabilizar uma avaliação quantitativa mais consistente dos trabalhos de laboratório apresentados pelos alunos.

A teoria matemática empregada nessas ferramentas adota uma abordagem simplista, porém eficaz na manipulação de medidas mecânicas e na quantificação das incertezas experimentais. Embora simplista, a abordagem matemática revela-se razoável e eficaz em trabalhos de laboratório, embora apresente algumas limitações.

Como é inerente a qualquer abordagem matemática desse tema, ela envolve um volume considerável de operações matemáticas, suscetíveis a erros, por mais simples que seja a teoria aplicada.

Este artigo apresenta a metodologia matemática utilizada nessas ferramentas, que, apesar de algumas limitações e imprecisões em determinadas circunstâncias, destaca-se por gerar resultados bastante razoáveis para a implementação no ensino superior e ser altamente modular.

Essa modularidade facilita a implementação dessa teoria em qualquer linguagem de programação que suporte o paradigma de orientação a objetos e a sobrecarga de operadores, ou mesmo por meio da programação funcional.

Este artigo tem como objetivo apresentar os fundamentos matemáticos subjacentes a essa teoria e, ao final, destaco duas implementações práticas, sendo uma em Python 3 e a outra um aplicativo de uma calculadora científica em Flutter.

Sobre o Ensino em Laboratório

De 2001 a 2021, desempenhei as funções de coordenador e responsável técnico pelo Laboratório de Física da UVV. Inicialmente, busquei implementar um método de ensino fortemente baseado na referência adquirida nos Laboratórios de Física da UFES (Universidade Federal do ES), composto por:

  1. Apresentação aos alunos de uma ferramenta para o desenvolvimento dos cálculos essenciais nos trabalhos de laboratório, destacando a base matemática apresentada neste artigo;
  2. Disponibilização de material com orientações para a elaboração de relatórios, enfatizando a avaliação e interpretação dos resultados, bem como análises gráficas;
  3. Fornecimento de roteiros com objetivos claros e instruções para a execução dos experimentos em laboratório;
  4. Avaliação baseada em relatórios que exploram os resultados obtidos nos experimentos, acompanhados por uma análise fundamentada.

Apesar de o processo parecer funcional na teoria, na prática as complexidades emergem. Erros mais evidentes nos procedimentos e no uso de equipamentos podem ser identificados e corrigidos durante a realização dos experimentos. Entretanto, pequenas variações nas disposições dos equipamentos e as numerosas possibilidades de erros nas operações matemáticas necessárias para atingir os resultados finais contribuem para uma considerável dispersão de resultados.

Ao final, esse processo pode se tornar exaustivo para os alunos, deixando pouca energia para a análise final dos resultados. Isso, por vezes, resulta em conclusões vagas e fracamente fundamentadas nos procedimentos realizados, ou mesmo na física do problema abordado.

É fato a importância de que os alunos compreendam os procedimentos matemáticos empregados nos cálculos dos seus resultados experimentais, bem como as limitações dos modelos matemáticos empregados. No entanto, isso não deve ser o objetivo último.

O LabCalc, conforme concebido, visa fornecer uma ferramenta que simplifica essa parte do trabalho, agilizando os processos matemáticos e permitindo um maior enfoque na análise e discussão dos resultados obtidos.

O método matemático adotado aqui representa uma simplificação de modelos clássicos, sem perdas significativas.

Vocabulário da Medida

Antes de adentrarmos na discussão do modelo matemático para o cálculo com incertezas, é crucial estabelecer uma nomenclatura básica sobre medidas e operações em laboratório. Não pretendo me estender demasiadamente nestes aspectos.

Valor Real

O Valor Real representa a medida exata de uma grandeza física, algo que, em geral, não existe. O Valor Real de uma medida só é alcançado em padrões, como um padrão de massa, comprimento ou tempo.

Considere um experimento para medir o comprimento de um objeto mantido sob temperatura e pressão constantes. Ao medi-lo em uma régua em centímetros, o valor lido na escala pode ser 12.5\,cm. Em uma régua em milímetros, o valor medido pode ser 12.45\,cm. Com o uso de um equipamento com precisão de 1 micrômetro, o valor medido pode ser refinado para algo como 12.458\,cm.

Seria possível estender esse processo com um equipamento ainda mais preciso até alcançar o Valor Real deste comprimento?

A resposta a esta pergunta é não. Mesmo que o objeto seja cortado com o melhor equipamento disponível na tecnologia atual, haverá um ponto em que as imperfeições da superfície serão detectadas pelo equipamento de medida, resultando em valores diferentes em medidas subsequentes do mesmo comprimento. Isso ocorre devido às pequenas imperfeições nas superfícies que são medidas pelo equipamento.

Em geral, isso pode ser observado ao tentar medir o diâmetro de uma esfera de aço com um micrômetro. A cada medida, se o equipamento for removido e reposicionado, pequenas variações de alguns mícrons serão notadas entre as diferentes medidas.

Valor Medido

Dessa forma, não há um valor real para o diâmetro de uma esfera, mas sim um Valor Medido. Este representa o valor obtido pelo equipamento utilizado, considerando as condições específicas no momento da sua execução.

A menos que estejamos em um laboratório de Padrões de Pesos e Medidas, lidamos exclusivamente com Valores Medidos.

Erro de Medida

Uma medida mecânica transcende a simples leitura de uma escala, envolvendo um conjunto de procedimentos destinados a minimizar erros procedurais ou mesmo acidentais, tais como:

  • Presença de impurezas na superfície do objeto a ser medido ou nas pinças do equipamento;
  • Necessidade de calibração;
  • Possibilidade de posicionamento incorreto do equipamento durante a medida;
  • Ocorrência de erro de paralaxe, quando a visualização da escala ocorre em um ângulo não reto;
  • Impacto de vibrações mecânicas no objeto de medida ou escala;
  • dificuldades ou impossibilidade de um posicionamento adequado da escala, entre outros fatores.

A discussão sobre erros de medidas é extensa, e não pretendo aprofundar-me nesse tópico, uma vez que não é o foco deste texto. No entanto, mesmo com condições operacionais ideais, superfícies meticulosamente limpas e operadores altamente qualificados, ainda enfrentamos as limitações mencionadas anteriormente.

De forma simplificada, esses erros operacionais introduzem uma imprecisão inerente à medida, que denominaremos aqui de incerteza.

Incerteza

A incerteza é uma tentativa de quantificar a confiabilidade do resultado de uma medida, estabelecendo um intervalo de validade para a medida. Esse intervalo deve conter o melhor valor possível para a grandeza medida, abrangendo tanto os erros operacionais quanto as limitações dos equipamentos, condições da medida ou imperfeições do objeto medido.

Metodologias e procedimentos para determinar a incerteza adequada em uma medida podem variar entre diferentes laboratórios, dependendo de suas metodologias, equipamentos e regras técnicas. Não é objetivo deste texto entrar nessas particularidades, deixando essa responsabilidade para os laboratórios determinarem suas próprias metodologias.

Com isso em mente, uma medida de comprimento pode ser expressa, com o uso de incerteza, da seguinte forma:

    \begin{equation*} m_0 = (12.56 \pm 0.03 )\,cm \end{equation}

Essa medida implica que qualquer valor entre 12.53,\text{cm} a 12.59,\text{cm} é igualmente provável para o Valor Medido deste comprimento. Assim, a incerteza expressa a medida na forma de uma faixa, neste caso, de \pm 0.03,\text{cm} em torno do valor central, 12.56,\text{cm}.

Ao lidar com incertezas, é crucial compreender que o valor 12.56,\text{cm} é tão válido quanto qualquer outro valor na faixa de 12.53,\text{cm} a 12.59,\text{cm}, e, portanto, não possui preferência sobre qualquer outro valor no intervalo.

Suponha que você realize um experimento para determinar a concentração de um determinado elemento em uma amostra por meio de medidas indiretas de outras propriedades físico-químicas da amostra. Após realizar as medidas das propriedades da amostra e empregar um modelo físico-químico para o problema, além de alguns cálculos, você obtém a resposta para este experimento como sendo:

    \begin{equation*} c = (11.66 \pm 0.08 )\,\text{Mol/L} \end{equation}

Isso significa que a concentração do elemento na amostra está compreendida entre 11.58 e 11.74,\text{Mol/L}.

Neste momento, a incerteza deve ser vista como um certificado de que o melhor Valor Medido para esta concentração, independentemente dos cuidados empregados na medida ou da qualidade do equipamento utilizado, deve necessariamente contemplar, ao menos, uma parte do intervalo indicado.

Caso contrário, ou ocorreu algum erro no procedimento experimental, ou o modelo aplicado é inadequado para a amostra, ou medida, em particular. Obviamente, qualquer uma das duas opções deve ser fundamentada em argumentos sólidos, e isso é essencialmente o que se espera em um trabalho experimental.

Uma discussão mais detalhada sobre erros e a determinação da incerteza pode ser encontrada em cursos de metrologia, onde esses são analisados minuciosamente e tratados de maneira adequada.

Cálculo com Incertezas

As próximas seções abordam a metodologia para realizar operações matemáticas com medidas e suas incertezas. O modelo apresentado é o mesmo introduzido nas disciplinas de laboratório de física em muitas universidades brasileiras, focado em simplicidade e modularidade para facilitar a implementação em ferramentas computacionais.

Soma

Seja A e B duas medidas

    \begin{equation*} A = a \pm \Delta a \end{equation}

    \begin{equation*} B = b \pm \Delta b \end{equation}

ou seja, a e b são as medidas e \Delta a e \Delta b são suas incertezas. A soma destas duas medidas pode ser calculada como:

    \begin{equation*} A + B & = & (a \pm \Delta a) + (b \pm \Delta b) \\ \end{equation}

(1)   \begin{equation*} A + B = (a + b) \pm (\Delta a + \Delta b) \end{equation*}

Portanto, a incerteza final será a soma das incertezas das duas medidas. A subtração segue o mesmo processo com uma pequena diferença: as incertezas sempre são somadas.

    \begin{equation*} A - B = (a \pm \Delta a) - (b \pm \Delta b) \end{equation}

(2)   \begin{equation*} A - B = (a - b) \pm (\Delta a + \Delta b) \end{equation*}

Ao final, seja na soma ou na subtração, as incertezas são somadas. Isso expressa que dividir um comprimento para medi-lo em várias etapas aumenta a incerteza do comprimento total, o que é razoável, visto que cada medida possui um erro operacional embutido.

Produto

Considerando as mesmas medidas A e B apresentadas anteriormente, agora desejamos determinar o produto A \cdot B. Multiplicando os elementos termo a termo, obtemos:

    \begin{eqnarray*} A \cdot B & = & (a \pm \Delta a) \cdot (b \pm \Delta b) \\ & = & a\cdot b \pm (a \cdot \Delta b + b \cdot \Delta a + \Delta a \cdot \Delta b) \end{eqnarray*}

Como, em geral, espera-se que \Delta a e \Delta b sejam significativamente menores que a e b, o último termo, \Delta a \cdot \Delta b, é bastante pequeno em comparação com os demais e pode ser negligenciado, ficando apenas com os dois primeiros elementos.

    \begin{eqnarray*} A \cdot B & = & a\cdot b \pm (a \cdot \Delta b + b \cdot \Delta a) \\ \end{eqnarray*}

Esta equação ainda pode ser convenientemente escrita na forma:

(3)   \begin{eqnarray*} A \cdot B & = & a\cdot b \left[ 1 \pm \left( \frac{\Delta a}{a} + \frac{\Delta b}{b}\right) \right] \end{eqnarray*}

Esta forma final é a mais fácil de ser implementada em operações matemáticas, além de explicitar outro elemento importante, tratado a seguir.

Incerteza Relativa

Esta expressão introduz um elemento muito útil e prático no cálculo com incertezas, a Incerteza Relativa. Ela é definida como a razão entre o Valor Medido e sua Incerteza:

(4)   \begin{equation*} IR_A = \frac{\Delta a}{a} \end{equation*}

Ou seja, a fração entre a incerteza e a medida.

Portanto, podemos compreender o produto A \cdot B como sendo o produto vezes a soma das incertezas relativas de A e B, como abaixo,

    \begin{eqnarray*} A \cdot B & = & a b \pm a b \left( IR_A + IR_B \right) \end{eqnarray*}

Outro uso interessante da incerteza relativa é o seu emprego como parâmetro de comparação de precisão entre duas medidas com incertezas, pois quanto menor a sua incerteza relativa, mais precisa é a medida. Isso é ilustrado no exemplo numérico abaixo:

    \begin{eqnarray*} A = 2.25 \pm 0.05 \Rightarrow IR_A & = & 0.05/2.25 = 0.022 = 2.2\% \\ B = 0.012 \pm 0.002 \Rightarrow IR_B & = & 0.002/0.012 = 0.167 = 16.7\% \end{eqnarray*}

Embora a incerteza de B seja muito menor que a incerteza de A, a medida A é mais precisa que B devido à sua menor incerteza relativa.

Potência

Agora, imagine que desejamos determinar o valor e a incerteza da potência A^3. Neste caso, podemos fazer isso empregando a regra do produto na expressão A \cdot A^2, como segue:

    \begin{eqnarray*} A^3 & = & A \cdot A^2 \\ & = & A \cdot \left\{ a a \left[ 1 \pm \left( \frac{\Delta a}{a} + \frac{\Delta a}{a} \right) \right] \right\} \\ & = & A \cdot a^2 \left[ 1 \pm 2 \frac{\Delta a}{a} \right] \\ & = & a \cdot a^2 \left[ 1 \pm \left(\frac{\Delta a}{a} + 2 \frac{\Delta a}{a} \right) \right] \\ & = & a^3 \left[ 1 \pm 3 \frac{\Delta a}{a} \right] \end{eqnarray*}

Em resumo, nesta expressão, vemos que a incerteza relativa de A^2 é 2 \Delta a/a, e de A^3 é 3 \Delta a/a. Por expansão para uma potência A^n, podemos esperar que sua incerteza relativa seja n \Delta a/a. Em uma extrapolação matemática, podemos afirmar que para qualquer n \in \Re, podemos esperar que:

(5)   \begin{equation*} A^n = 1 \pm |n| \frac{\Delta a}{a} \end{equation*}

O módulo de n é necessário para potências negativas, já que a incerteza deve ser sempre positiva.

Divisão

Neste ponto, a divisão pode ser facilmente determinada empregando a incerteza relativa da potência acima juntamente com um produto:

    \begin{eqnarray*} \frac{A}{B} & = & \frac{a}{b} \left[ 1 \pm \left( IR_A + IR_{B^{-1}} \right) \right] \\ & = & \frac{a}{b} \left[ 1 \pm \left( \frac{\Delta a}{a} + |-1|\frac{\Delta b}{b} \right) \right] \end{eqnarray*}

ou seja

(6)   \begin{equation*} \frac{A}{B} = \frac{a}{b} \left[ 1 \pm \left( \frac{\Delta a}{a} + \frac{\Delta b}{b} \right) \right] \end{equation*}

Expressões Gerais

Como já deu para se observar, o cálculo da incerteza em uma operação envolvendo produtos, divisões e potências resume-se a efetuar a operação e determinar sua incerteza como sendo o resultado da operação vezes a soma das incertezas relativas. Desta forma, o produto \sqrt{A/B^5} \cdot C^3, onde A, B e C são medidas com suas respectivas incertezas, pode ser determinado como:

(7)   \begin{equation*} \sqrt{\frac{A}{B^5}}\cdot C^3 = \sqrt{\frac{a}{b^5}} \cdot c^3\left[1 \pm \left(\frac{1}{2}\frac{\Delta a}{a} + \frac{5}{2}\frac{\Delta b}{b} + 3\frac{\Delta c}{c} \right) \right] \end{equation*}

Funções Transcendentais

Para funções que não podem ser representadas por polinômios, a proposta aqui é utilizar a média dos valores nos extremos do argumento como valor e metade da variação como incerteza. Em outras palavras, se X = x \pm \Delta x representa um valor com sua incerteza, as expressões a seguir representam o valor de uma função f(x) aplicada em X:

(8)   \begin{equation*} f(X) = \frac{f(x+\Delta x) + f(x - \Delta x)}{2} \end{equation*}

e sua incerteza,

(9)   \begin{equation*} \Delta f(X) = \frac{|f(x+\Delta x) - f(x - \Delta x)|}{2} \end{equation*}

O problema desta solução surge quando a medida X = x \pm \Delta x envolve um ponto de máximo ou mínimo da função f(x). Uma forma de contornar isto seria avaliar a função em seu máximo/mínimo e usar este valor como um dos extremos para a função.

Para uma aplicação modular como é proposto neste artigo, as únicas funções que podem gerar este problema seriam as funções seno e cosseno em torno de um ponto de máximo ou mínimo.

Contornando Máximos/Mínimos em Seno e Cosseno

Neste caso, imagine que se deseja determinar o f(X) de uma medida X = x \pm \Delta x em que este intervalo envolve um máximo ou mínimo da função. Inicialmente, é necessário determinar se no intervalo existe um máximo ou mínimo. Isto é facilmente verificado observando as derivadas das funções em x - \Delta x e x + \Delta x.

Caso não haja nenhum máximo ou mínimo no intervalo, é esperado que as derivadas da função nos extremos do intervalo sejam as duas crescentes ou as duas decrescentes, fazendo com que o produto destas derivadas seja sempre positivo. Porém, se houver um máximo ou mínimo no intervalo, o produto das derivadas nos dois extremos do intervalo será sempre negativo, visto que antes de um máximo, a função é crescente e após o máximo, a função é decrescente, e o contrário ocorre no caso de um mínimo no intervalo.

Para facilitar, considere a função do gráfico da figura abaixo, em que x \pm \Delta x envolve um máximo. As linhas verde e vermelha no gráfico a seguir ilustram as derivadas da função no início e no final do intervalo, indicando um máximo no intervalo.

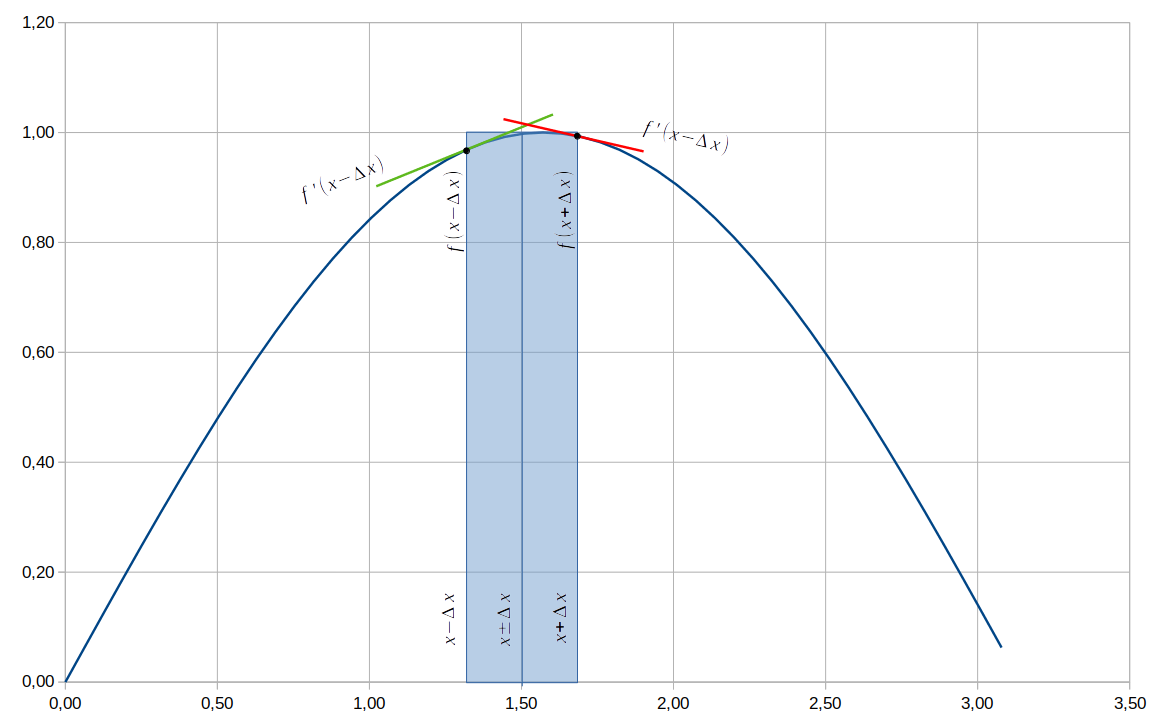
Em seguida, determina-se qual o valor de f(x-\Delta x) ou f(x+\Delta x) se encontra mais distante do máximo. No gráfico acima, f(x-\Delta x) está mais distante. Desta forma, o f(X) será definido como:

(10)   \begin{equation*} f(X) = \frac{f_{max} + f(x - \Delta x)}{2} \end{equation*}

e a sua incerteza,

(11)   \begin{equation*} f(X) = \frac{|f_{max} - f(x - \Delta x)|}{2} \end{equation*}

Onde f_{\text{max}} é o valor máximo da função no intervalo.

Obviamente fazer isto manualmente pode ser bem tedioso, mas a ideia é facilmente implementada em uma linguagem de computação.

Código python

Recentemente, atualizei um módulo em Python 3 para o Measure, disponível em github.com/rudsonalves/measure.git. O projeto está em estágio inicial, mas já é funcional.

Para utilizá-lo, basta invocar o Python 3 e importar o módulo Measure, localizado em measure/measure.py. Seu terminal Python funcionará como uma calculadora.

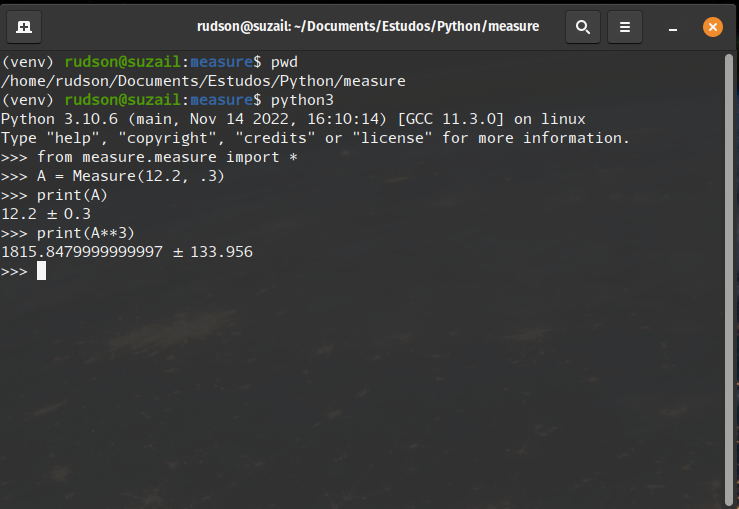
Futuramente, pretendo implementar outras funcionalidades ao módulo, como truncamento e mais funções.

Calculadora em Flutter

Uma versão preliminar da calculadora em Flutter já está funcional e aguarda a moderação do Google Play para ser disponibilizada. Assim que tiver mais informações atualizo aqui.

Este post tem um comentário

Deixe um comentário

Esse site utiliza o Akismet para reduzir spam. Aprenda como seus dados de comentários são processados.